FIR Filters
Cascading Two FIR Filters
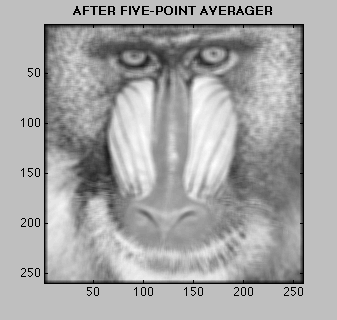
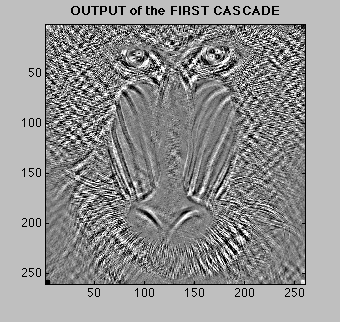
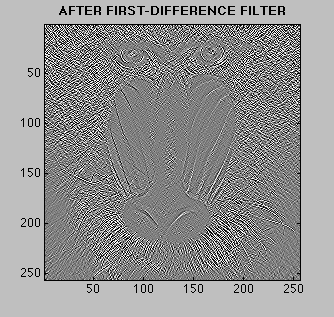
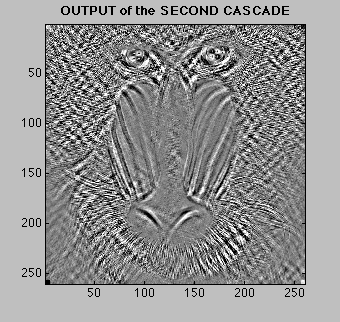
When you cascade two FIR filters together, the output of the first becomes the input to the second. The order does not matter. Either filter can be placed first, it makes no difference. The final result is the same even though the intermediate results are different. The figures below can help you see this idea with two cascaded filters. Note how \(v[n]\) (in the top) differs from \(w[n]\) (in the bottom) but see how \(y_1[n]\) and \(y_2[n]\) are identical. You can also click on the filters to see their respective frequency responses. Click Here |
Click Here |
 Click Here |
Click Here |
 Click Here |
 |
 |
 |
 |
 |
 Click Here |
Click Here |
 Click Here |
Click Here |

Click Here |
 |
 |
 |
 |
 |
Adding the Outputs of two FIR Filters
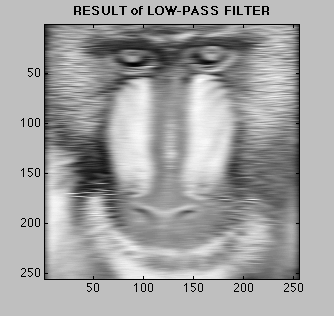
We can also add the outputs of two or more FIR filters and see the combined effect. An informative experiment is the following: Filter the signal with low-pass filter. Then filter the original signal with a special high-pass filter having the same cutoff frequency (called a complementary filter). Now when you add up the two results, you get original signal back! The system below exhibits this idea on an image. Click on the various parts of the system to see how it works. |
 |
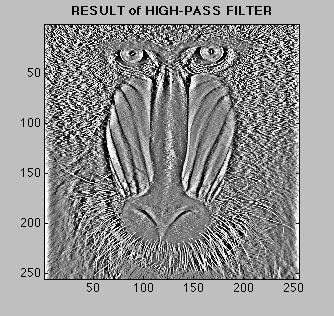 |
|
 Click Here |
Click Here |
Click Here |
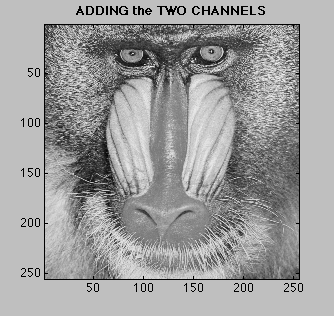 |
 |
 Click Here |
||
 Click Here |
Click Here |
 Click Here |
|
 |
 |
 |
