In this appendix, we describe the mathematical theory of Fourier series. We use specific examples of pulse waves, triangular waves, and rectified sinusoids to show how the Fourier series representation is obtained and how each signal's spectrum is defined by the Fourier series. Finally, we focus on general properties of the Fourier series which not only extend the understanding of the frequency domain, but also make the job of signal analysis easier in practice. Parseval's theorem and the approximation error from finite synthesis are discussed.

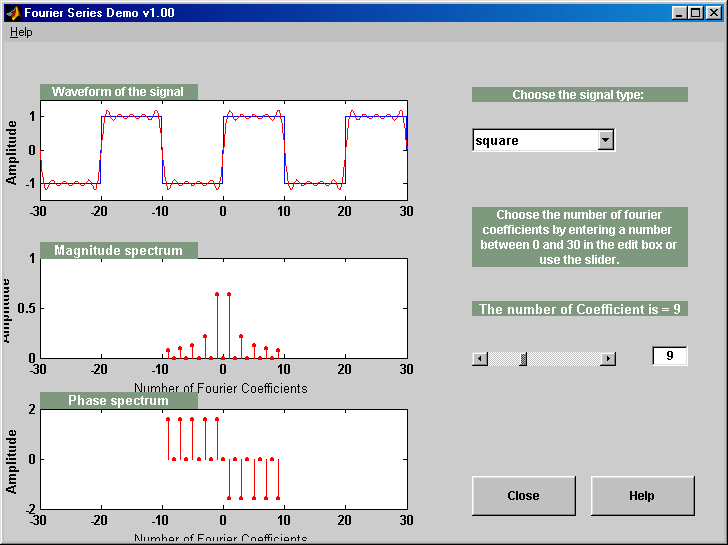
Demos - MATLAB 1