Hint 2

1. Find the amplitude.
2. Find the period.
   by measuring the time distance between peaks.
3. Calculate the frequency from the period.
4. Find the phase.
   by measuring the time of a peak.

To find the phase, note the time shift of a peak (sometimes called delay). What is it for this plot?



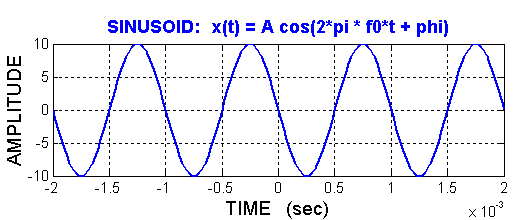
I get \(0.25\) ms to the left, which is \(t_1 = -0.25\) ms.
What is the relationship between the phase angle, \(f\), and the time shift, \(t_1\)?
Recall that there are two ways of writing cosines, how do \(f\) and \(t_1\) relate?

\(A \cos(2 \pi f_0 t + f) = A \cos(2 \pi f_0 ( t-t_1 ))\)

Now we can equate the arguments of the two cosines: \(2 \pi f_0 t + f = 2 \pi f_0 ( t-t_1) \)

which leads to   \(f=-2\pi f_0 t_1\)

Knowing the frequency and the time of the peak, you can calculate \(f\) now.