There are four FM (Frequency Modulation) sounds to study. First listen to each of them without knowing how they differ.

Each one of these FM signals is synthesized from the same basic formula: a sine-wave in the argument of a cosine function is used to "modulate" the frequency at the rate fm.

$$x(t) = A \cos( 2\pi f_c t + D_f \cos(2\pi f_m t) )$$

However, the fundamental idea of instantaneous frequency breaks down in this case because the chirp rate gets too high.

Sounds in time-frequency domain

Let's look at the sounds in the time-frequency domain to see how the spectrum changes with increasing chirp rate.

Wideband FM can be Tricky

Listen to each of the signals again by clicking on the waveform. Keep in mind that only the chirp rate is changing. In all cases, the \(f_i(t)\) formula predicts that the instantaneous frequency would oscillate between \(400\) Hz and \(700\) Hz.


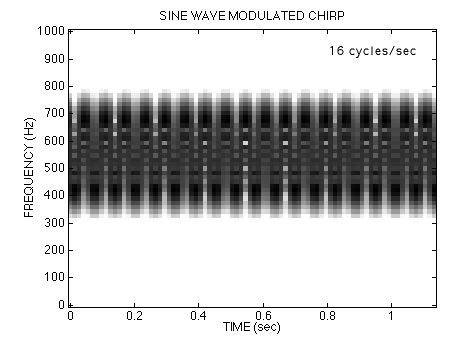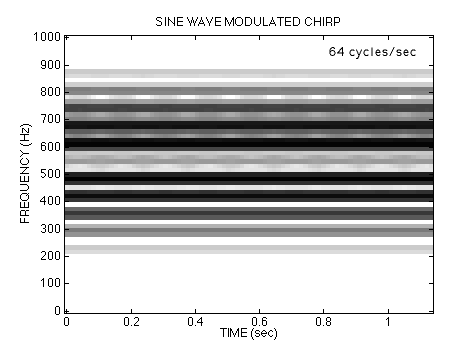Doesn't the \(64\) cycle case sound like a vowel – maybe "aaah" or "owe" ?

Notice that the previous ideas about the frequency content of the FM signal are no longer valid !

If the modulation rate gets too large, then our perception of the sounds changes. However, the change is not necessarily a loss, since the chirps created with high-frequency sine waves in their argument seem to posses a harmonic quality (i.e., the spectrum exhibits a number of isolated spectral lines). This fact is the basis of FM synthesis for various musical instruments.

Carson's Rule:

Carson's rule gives the bandwidth of an FM signal as an approximation that sort of works for both narrow band and wideband cases. Let \(f_m\) be the highest frequency in the modulating signal. Let \(D_f\) be the maximum frequency deviation, which is related to the amplitude of the modulating signal. Let \(f_c\) be the carrier frequency. Then the bandwidth (\(BW\)) of the FM signal (centered on \(f_c\)) is $$BW = 2(f_m + D_f)$$ Thus for narrow band FM, \(D_f\rightarrow 0\) and \(BW =2f_m\). For wideband FM, \(D_f \gg f_m\) and \(BW = 2D_f\). Sometimes you see the formula given in terms of "\(\beta\)", where \(\beta=\frac{D_f}{f_m}\).$$BW = 2(1+\beta)f_m,$$ Beta can also be related to a parameter of Bessel functions that arise when you use as the signal model $$x_{FM}(t) = \cos( 2\pi f_c t + \beta \sin(2\pi f_m t) )$$ If you differentiate the instantaneous frequency of this signal you get $$f(t) = \frac1{2\pi} \frac{d\theta (t)}{dt} = f_c + \beta f_m \cos(2\pi f_m t)$$ so \(\beta f_m = D_f\), the maximum frequency deviation about the carrier.