Chirp Synthesis Demo

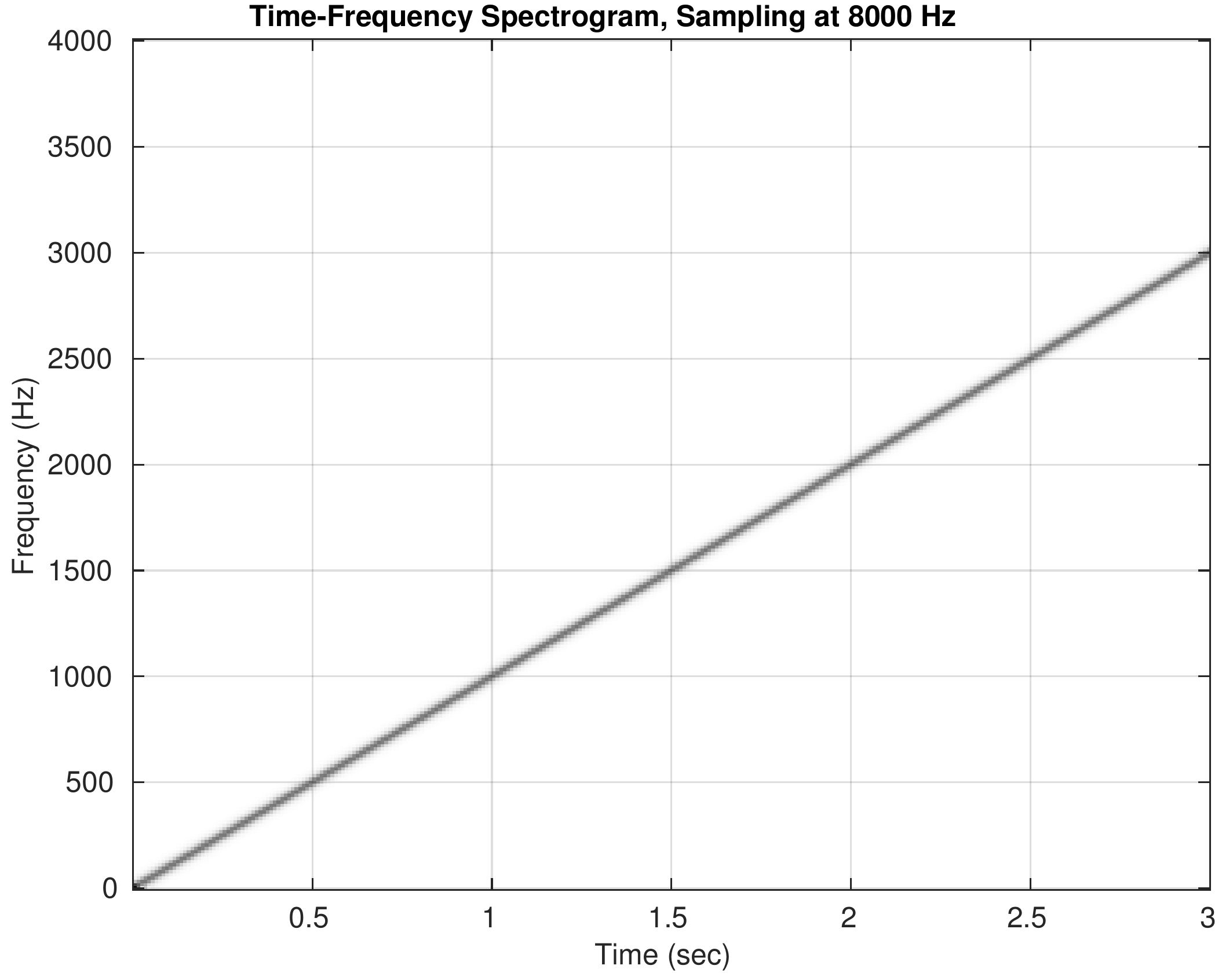
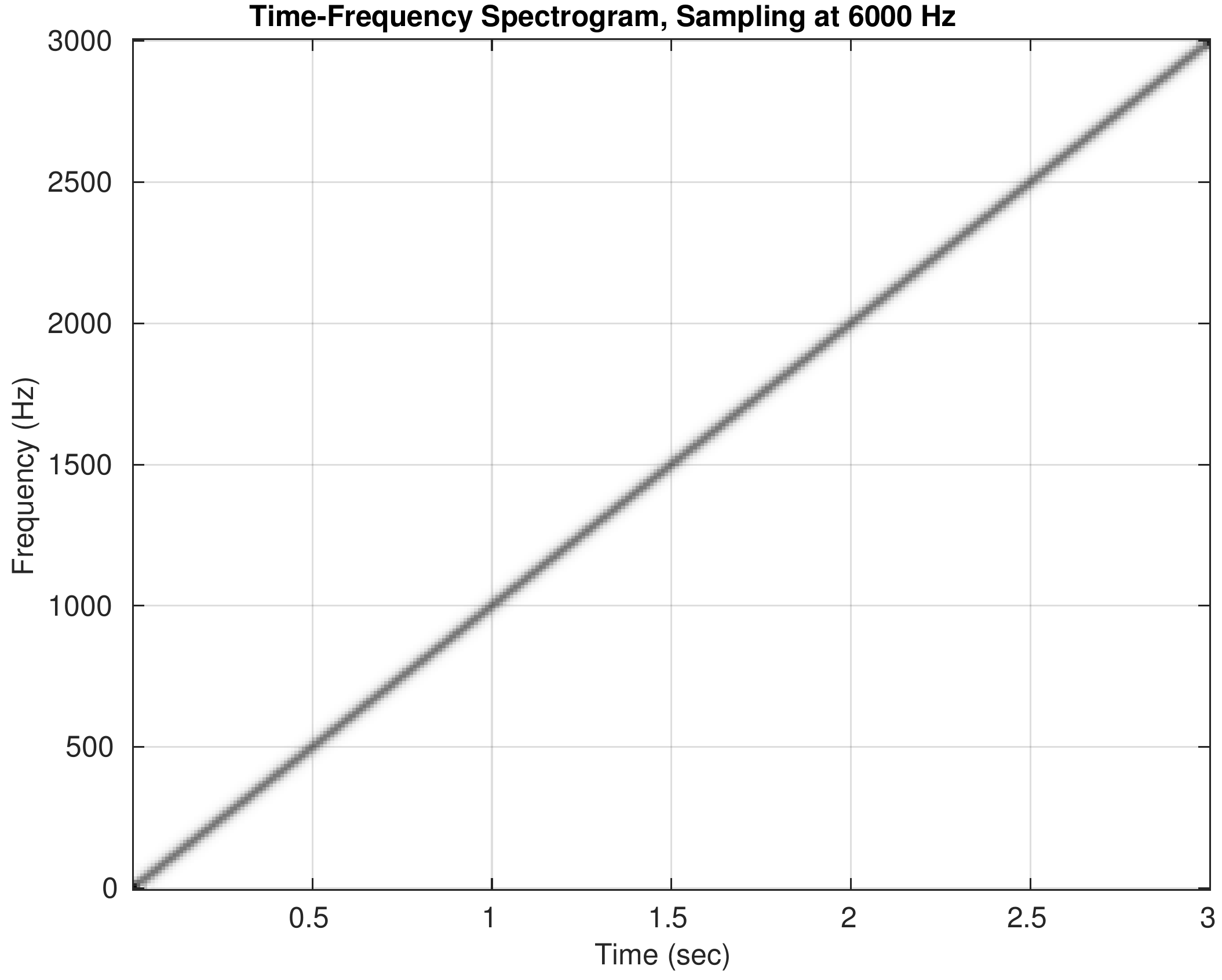
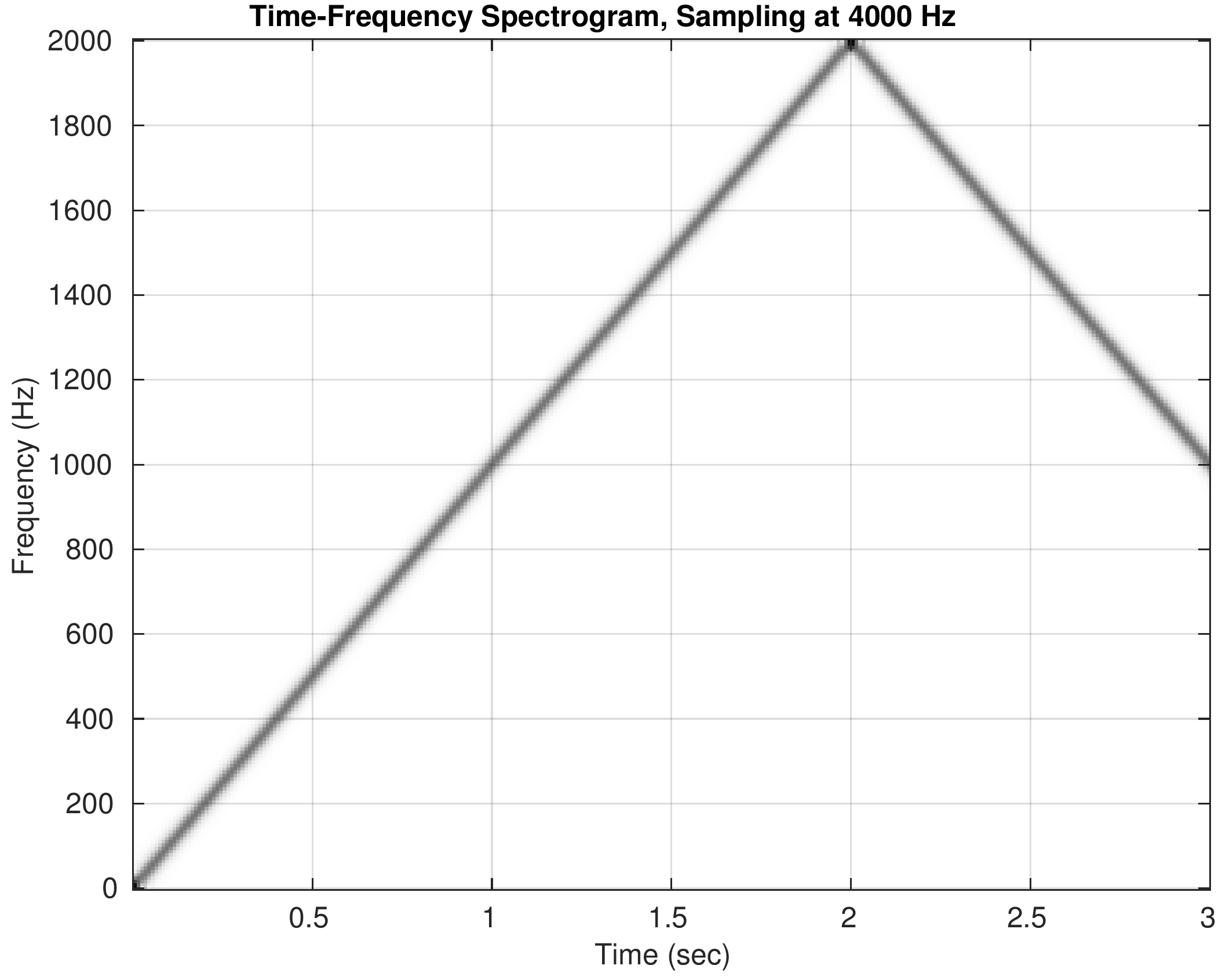
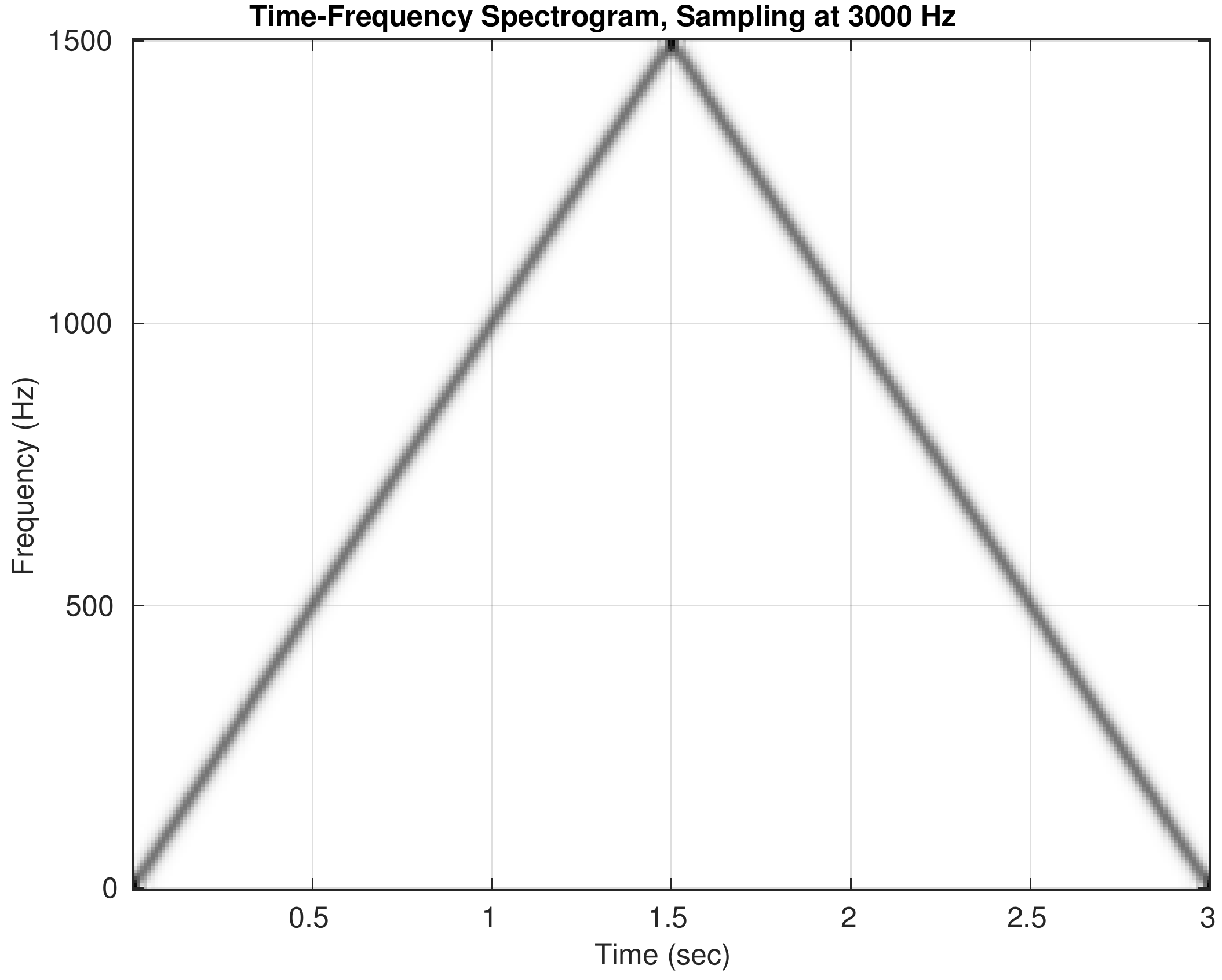
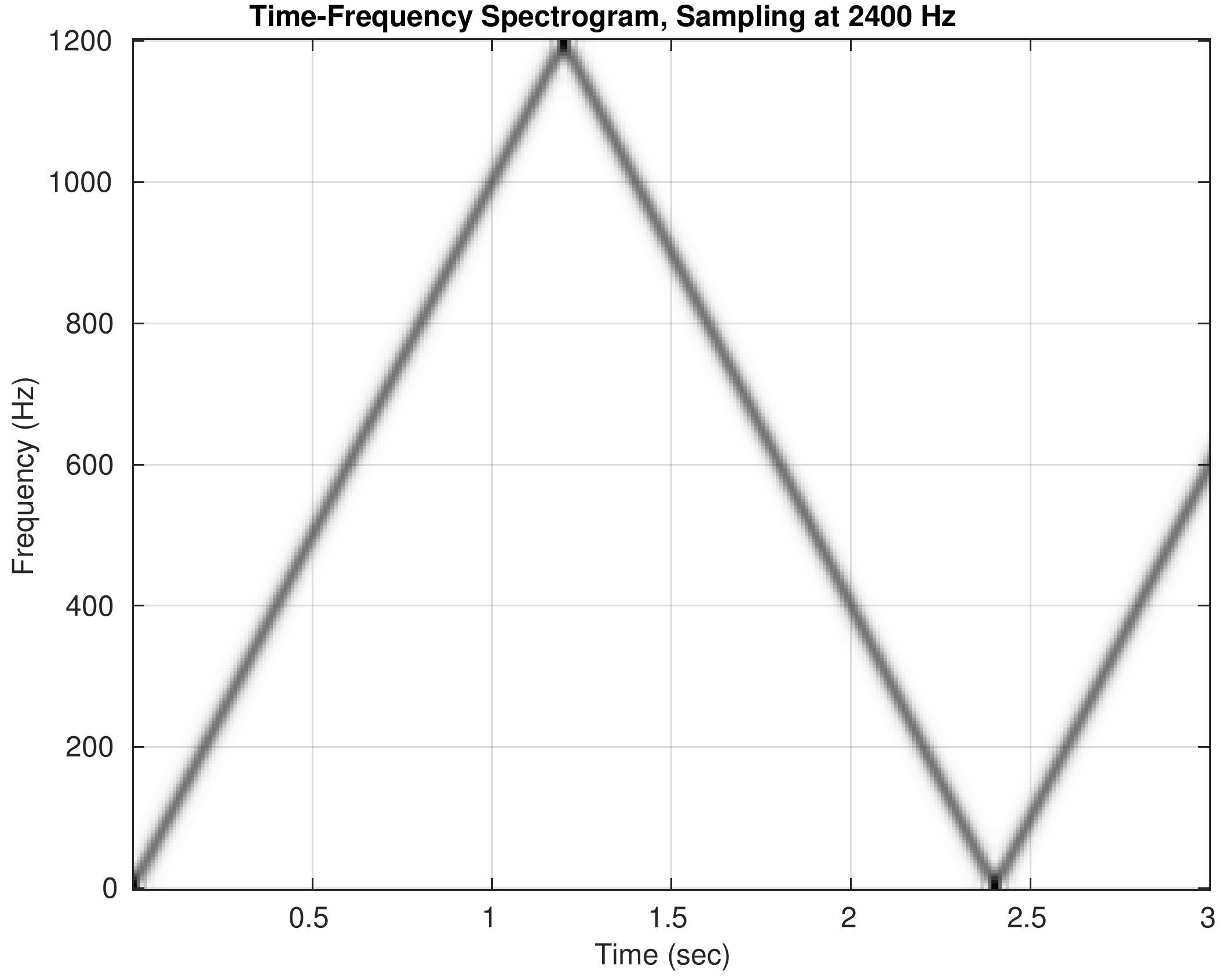
A linear-FM (chirp) signal is an ideal test signal to explore the concept of aliasing due to sampling. By visualizing the spectrogram of a synthesized chirp and listening to the sound, we experience the fact that a D-to-C converter cannot create output signals with frequencies higher than one half of the sampling frequency. Consult Section 4-2.5 Maximum Reconstructed Frequency for more discussion of this issue. This chirp synthesis demo consists of two simple components (a C-to-D converter and a D-to-C converter) and four steps:

Use the mathematical formula for a continuous-time chirp signal $$ x(t) = \cos( \pi\alpha t^2 )\qquad 0\leq t \leq T $$ to define a signal whose chirp rate is $\alpha$Hz/s, whose duration is $T$ seconds.
Produce a discrete-time signal by sampling $x(t)$ at a rate $f_s$ samples/s. This is done by evaluating $x(t)$ at $t=n/f_s$, and is, in effect, a C-to-D converter. The result is $x[n] = x(n/f_s)$.
Use Matlab's soundsc function to play the signal for listening. This is the D-to-C conversion component because a continuous-time signal must be created from $x[n]$ in order to drive the audio output, i.e., the speakers.
Evaluate and display the spectrogram of $x[n]$, which gives a visualization of what we hear.

In the demo, the chirp rate is $\alpha = 1000$ Hz/s, and the time duration is $T=3$s, so the instantaneous frequency $(f_i(t) = \alpha t)$ goes from zero at $t=0$ to $3\alpha = 3000$Hz at $t=3$s. Since the highest frequency in $x(t)$ is $3000$Hz, there should be no aliasing if $f_s\geq 6000$Hz.

The demo shows what happens for five different sampling frequencies: 8000, 6000, 4000, 3000, and 2400 Hz. The first two cases exhibit no aliasing and the sound rises from 0 to 3000 Hz. In the last three cases, the sound goes up and down because $f_s/2<3000$Hz. When $f_s=4000$, the maximum output frequency is $2000$Hz, for $f_s=3000$, the maximum output frequency is $1500$Hz, and for $f_s=2400$, the maximum output frequency is $1200$Hz.

Spectrograms for the five cases are shown below. Click on the spectrogram to hear the corresponding chirp. Note the different $y$-axis scales for frequency. When you listen to the sounds, try to follow the ups and downs that match the spectrograms.