y1_output_5pt

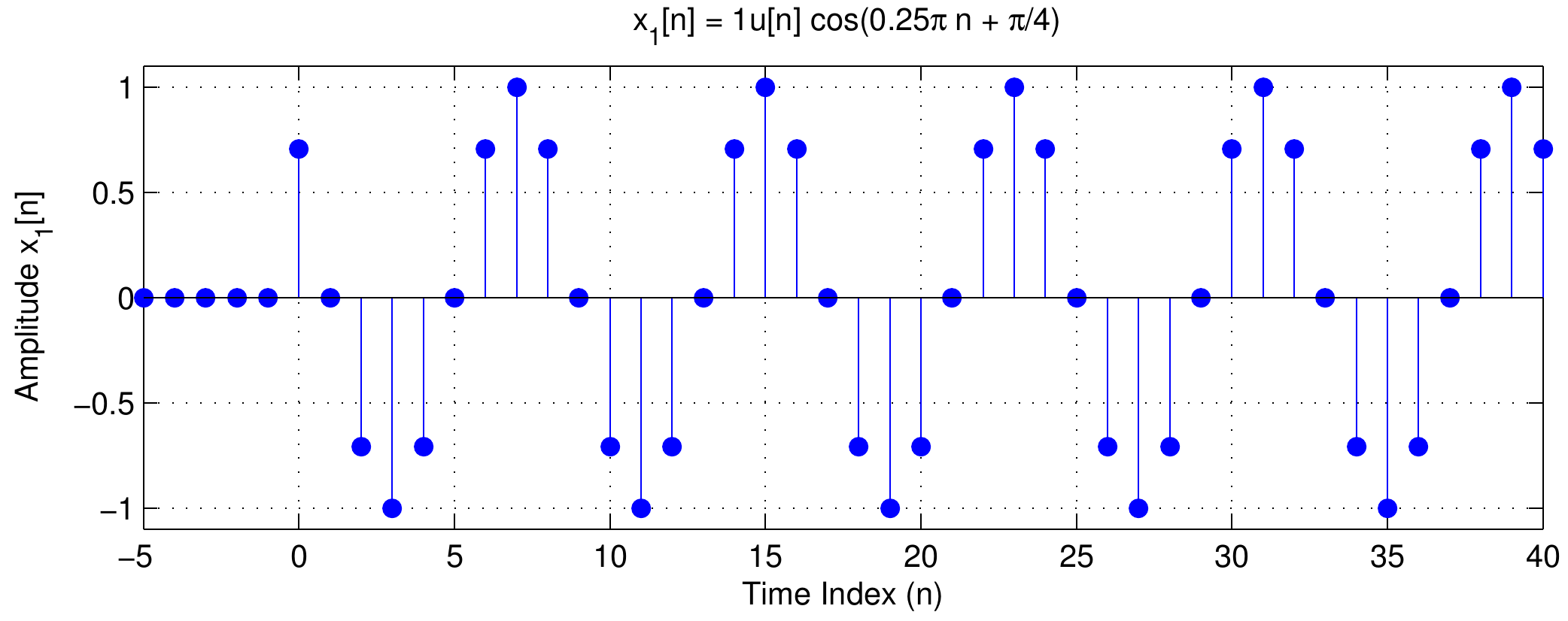
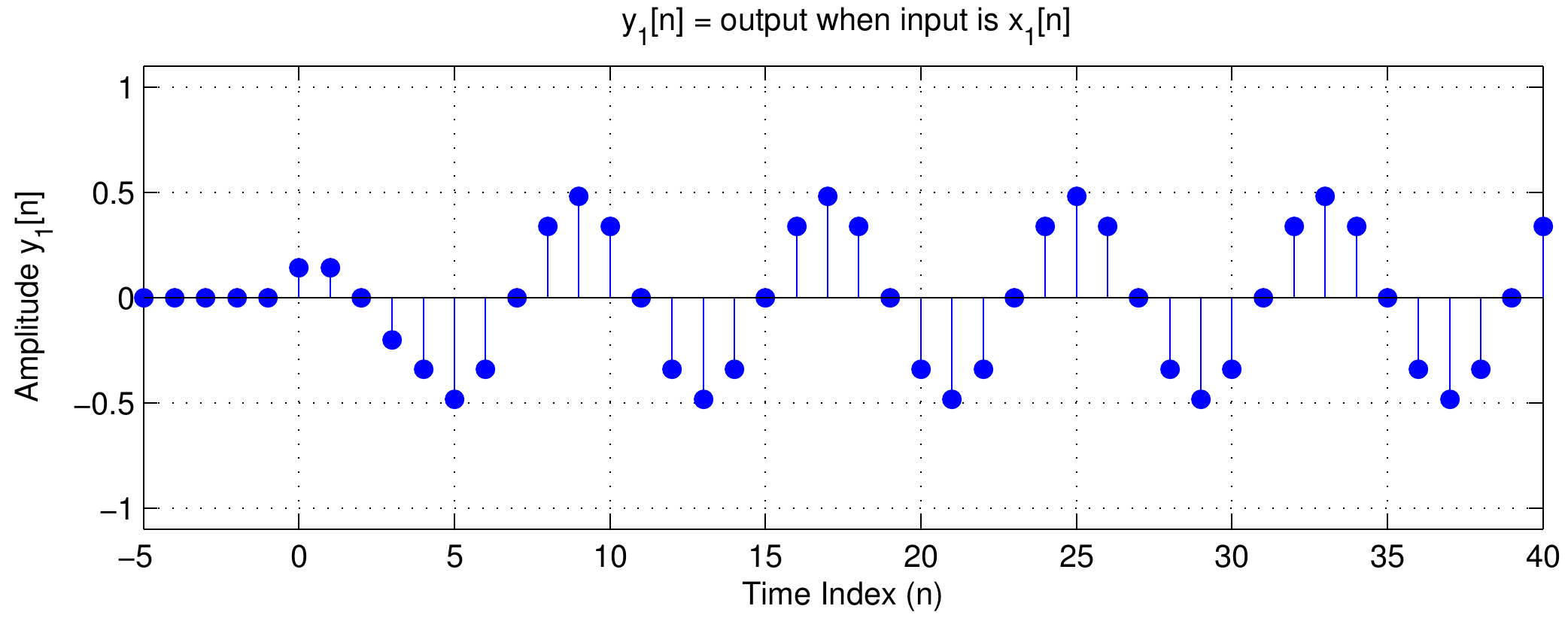
Figure 1: Comparison of input and output waveforms for the five point averager filter. Click on either waveform to hear how it sounds. Assuming the A/D and D/A converters use a sampling rate of 8000 Hz. what frequency do you expect the tones to have?

While the frequency of the output tone remains unchanged, it has been modified by a complex scale factor. In order to determine this scale factor, the frequency response of the five point averager filter must be evaluated at the frequency of interest:

\(H(\hat\omega)|_{\hat\omega=0.125\pi} =(\frac{sin(\hat\omega5/2)}{5sin(\hat\omega/2)}) e^{-j2\hat\omega}|_{\hat\omega=0.125\pi} =0.8524e^{-j\pi/4}\)
Therefore,
\(y_1 = \mathfrak Re\{0.8524e^{-j\pi/4} 2e^{j 0.125\pi n+\pi/3}\} =1.7048cos(0.125\pi n + \pi/12)\)