Overview: In chapter six the frequency reponse function for FIR
filters is introduced.
When a pure sinusoid passes through a linear time-invariant filter, the
output is a sinusoid at the same frequency, but its magnitude and phase
might be changed.
In this chapter, we derive the frequency response formulas for several
common FIR filters.
Plots of the magnitude and phase versus frequency summarize how the
filter treats sinusoidal inputs over the entire range of possible
input frequencies.
Finally, the concept of filtering is introduced.
Since all signals can be decomposed into sinusoidal components,
the frequency response function characterizes frequency regions called
stop bands and pass bands, where the
FIR filter will reject signal components or pass them nearly undistorted.
Image porcessing examples are used to show the effect of filtering as
blurring for low-pass filtering and sharpening for high-pass.
In later chapters and later courses, methods of (optimal) filter design will be introduced,
so that the filter coefficients can be chosen to achieve a
desired frequency response characteristic.
Demos - MATLAB 3
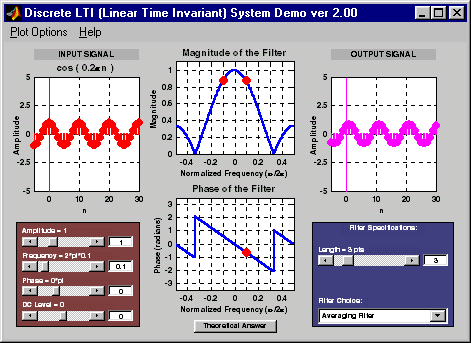
DLTIDemo is a program that illustrates the relationship between the input
and output of a discrete-time linear time-invariant (LTI) filter
when the input is a sinusoidal function.
The user is allowed to control the parameters of both the input sinusoid and the digital filter.
Demos - LabVIEW 2
The Dirichlet function Demo lets you look at how changing L changes the Dirichlet function.
Illustrates the sinusoid-in gives sinusoid-out concept.
Labs - MATLAB 4
The goal of this lab is to study the frequency response. For FIR filters this is the response to inputs such as
complex exponentials and sinusoids. You can use
firfilt(), or conv(), to implement filters and freqz()
to obtain the filter’s frequency response. As a result, you should learn how to characterize a filter by
knowing how it reacts to different frequency components in the input.
The goal of this lab is to study the response of FIR filters to
inputs such as complex exponentials and
sinusoids. In the experiments of this lab, you will use
firfilt(),
or conv(), to implement filters and
freqz() to obtain the filter's frequency response.
As a result, you should learn how to characterize a
filter by knowing how it reacts to different frequency components
in the input.
This lab also introduces two practical filters: bandpass filters
and nulling filters. Bandpass filters can be
used to detect and extract information from sinusoidal signals, e.g.,
tones in a touch-tone telephone dialer.
Nulling filters can be used to remove sinusoidal interference, e.g.,
jamming signals in a radar.
The goal of this lab is to study the sinusoidal response of some simple FIR filters in Matlab.
This leads to a study of the frequency response function.
In the experiments of this lab, you will use the Matlab GUI called
dltidemo to find the frequency
response function for FIR filters.
[Files]
In this mini-project you will write a simple Matlab
program that removes unwanted tones from a wav file.
The file
SunshineSquare.wav has had some unwanted tones added to it.
Your job is to remove the tones so you can hear the message better.
[Files]
Labs - LabVIEW 4
The goal of this lab is to study the response of FIR filters to
inputs such as complex exponentials and
sinusoids. In the experiments of this lab, you will use firfilt(),
or conv(), to implement filters and
freqz() to obtain the filter's frequency response. As a result,
you should learn how to characterize a
filter by knowing how it reacts to different frequency components in the input.
This lab also introduces two practical filters: bandpass filters
and nulling filters. Bandpass filters can be
used to detect and extract information from sinusoidal signals, e.g.,
tones in a touch-tone telephone dialer.
Nulling filters can be used to remove sinusoidal interference, e.g.,
jamming signals in a radar.
This lab introduces a practical application where sinusoidal
signals are used to transmit information: a touchtone
dialer. Bandpass FIR filters can be used to extract the
information encoded in the waveforms. The goal
of this lab is to design and implement bandpass FIR filters in MATLAB,
and do the decoding automatically.
In the experiments of this lab, you will use
firfilt(), or conv(),
to implement filters and freqz() to
obtain the filter's frequency response. As a result,
you should learn how to characterize a filter by knowing
how it reacts to different frequency components in the input.
[Files]
This lab introduces a practical application where we attempt
to extract information from sinusoidal signals -
in this case, piano notes. Bandpass FIR filters can be
used to extract the information encoded in the waveforms.
The goal of this lab is to design and implement several
bandpass FIR filters in MATLAB, and use the
filtered outputs to determine automatically which note is being played.
However, since there are 88 keys on
the piano, we will only require the system to figure
out which octave the note is in, not the exact note. In
the experiments of this lab, you will use
firfilt(), or conv(),
to implement filters and freqz() to
obtain the filter's frequency response. As a result,
you should learn how to characterize a filter by knowing
how it reacts to different frequency components in the input.
[Files]
In this mini-project you will Write a simple LabVIEW
VI that removes unwanted tones from a wav file.
The file SunshineSquare.wav has had some unwanted tones added to it.
Your job is to remove the tones so you can hear the message better.
[Files]