7. Discrete-Time Fourier Transform

Overview: Here the discrete-time Fourier transform (DTFT) is introduced along with the inverse DTFT. Transform pairs and properties are developed. The transform method solves the input-output problem for a filter by exploiting the convolution property of the DTFT which converts the convolution $y[n]=x[n]\ast h[n]$ to a multiplication of DTFTs, $$Y(e^{j\hat\omega})=X(e^{j\hat\omega})H(e^{j\hat\omega})$$ The frequency response is therefore understood to be the DTFT of the impulse response. Ideal filters are presented along with the window method of FIR filter design in which the impulse response of an ideal filter is truncated and weighted with window coefficients.

Databases: Labs Examples Exercises Homework Search

Demos - MATLAB 2

DTFT Pairs Demo

A table of DTFT pairs is usually given as a list of formulas for the signal $x[n]$ and its DTFT $X(e^{j \hat\omega})$. These formulas can be visualized as plots, and this demo focuses on the ability to recognize signals and transforms in a graphical form.

Filter Design Demo

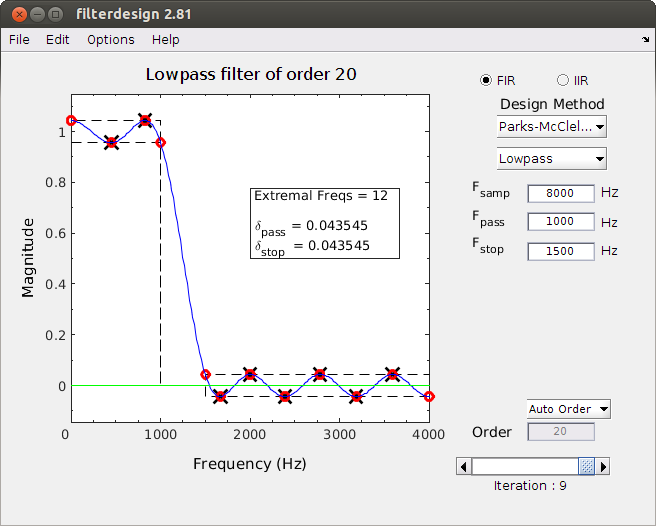
The Filter Design Demo is a program that designs simple FIR (and IIR) digital filters, along with tutorial visualizations of the filter design process.

Features:

FIR Design with many different window types
Numerous plot options: magnitude/phase response, pole-zero diagram, and impulse response
IIR Design of Butterworth filters
Parks-McClellan FIR Design showing the iterations of the Remez Exchange method

Labs - MATLAB 2

P-13: Encoding and Decoding Touch-Tone (DTMF) Signals

This lab introduces a practical application where sinusoidal signals are used to transmit information: a touch-tone dialer. Bandpass FIR filters can be used to extract the information encoded in the waveforms. The goal of this lab is to design and implement bandpass FIR filters in M ATLAB , and to do the decoding automatically. In the experiments of this lab, you will use firfilt(), or conv(), to implement filters and freqz() to obtain the filter’s frequency response. 1 As a result, you should learn how to characterize a filter by knowing how it reacts to different frequency components in the input. [Files]

S-6: FIR Filter Design GUI

The goal of this lab is to learn some methods for designing practical FIR filters in Matlab. These filters will have a finite number of coefficients, and a frequency response that approximates an ideal frequency response shape.