Overview: In this chapter the class of infinite-impulse-response (IIR)
filters is introduced. These digital filters involve feedback terms because
past values of the output signal are used to compute the present output.
The terminology "recursive filter" is also used to name these filters. Their
\(z\)-transform system functions are rational functions which have poles
and zeros. Insight into the important properties of these filters comes
directly from the pole-zero representation.
Demos - MATLAB 5
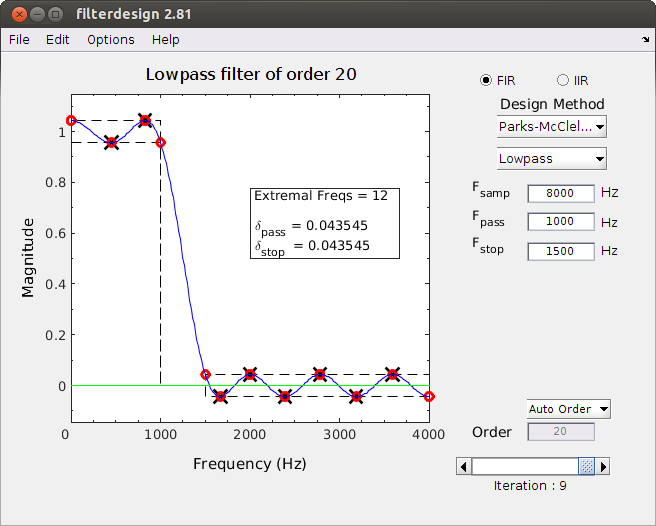
The Filter Design Demo is a program that designs simple IIR (and FIR) digital filters,
along with tutorial visualizations of the filter design process.
Features:
- IIR Design of Butterworth filters
- Numerous plot options: magnitude/phase response, pole-zero diagram, and impulse response
- FIR Design with many different window types
- Parks-McClellan FIR Design showing the iterations of the Remez Exchange method
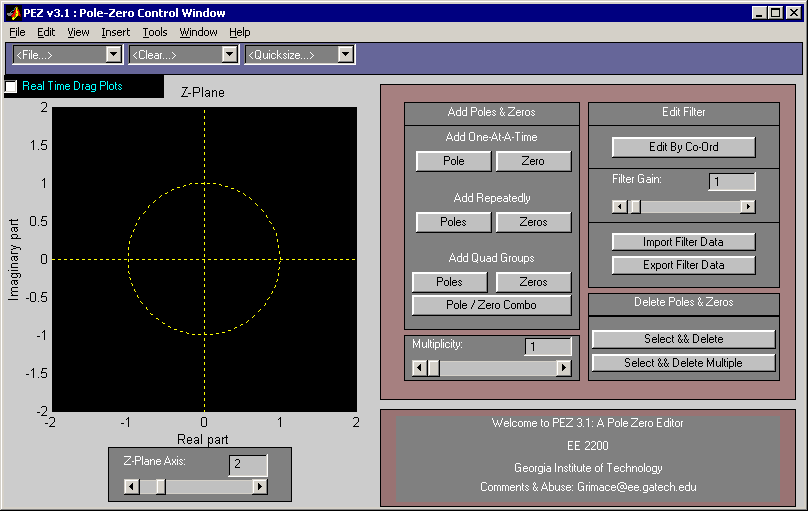
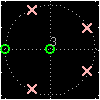
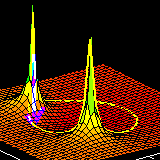
PeZ (pezdemo) is a MATLAB tool for pole/zero manipulation.
Poles and zeros can be placed anywhere on a map of the
\(z\)-plane.
The corresponding time domain (\(n\)) and frequency
domain (\(\hat\omega\)) plots will be displayed.
When a zero pair (or pole pair) is dragged, the
impulse response and frequency response plots will
be updated in real time.
Demos - LabVIEW 0
Labs - MATLAB 6
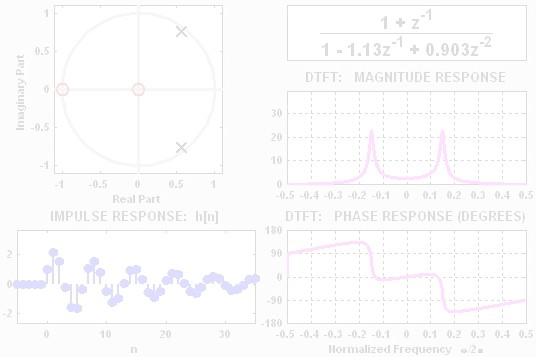
The objective for this lab is to build an intuitive understanding of
the relationship between the location of poles and zeros in the
z-domain, the impulse response \(h[n]\) in the \(n\)-domain,
and the frequency
response \(H(e^{j\hat\omega})\) (the \(\hat\omega\)-domain). A
graphical user interface (GUI) called
PeZ was written in MATLAB
for doing interactive explorations of the three domains.
The goal of this lab is to explore the connection between the time domain (n), the frequency domain (\(\hat\omega\)),
and the z-transform domain, using the GUI PeZ in MATLAB.
- Placing Zeros: When placed on the unit circle, zeros of \(A(z)\) will force the frequency response to be zero which can then be used to null out sinusoids at one frequency.
- Placing Poles: When placed near the unit circle (but inside), roots of \(B(z)\) will create peaks in the frequency response which can be used to form BPFs.
- Designing IIR Notch Filters: requires conjugate zeros on the unit circle (UC) with a poles at the same angle, just inside the UC. The frequency response of the notch is much sharper than a nulling filter which is an FIR filter formed only from the conjugate zeros on the UC.
In this mini-project you will experiment with PeZ to learn the connection
between pole-zero placement and frequency response. Given this information
you will redo the Tone Removal Mini-Project using an IIR.
For this mini project you will write a simple function that
listens to a tone and identifies what note it is.
[Files]
For this mini project you will write a simple function that
listens to a wav file of a simple song and identifies
the notes being played.
The wav files have some simple songs on which you can practice.
[Files]
You have gotten to the point in your studies that you can
understand DSP papers that appear in IEEE publications.
The purpose of this project is to read one such paper
and reproduce some of its results.
Labs - LabVIEW 7
The objective for this lab is to build an intuitive understanding of
the relationship between the location of poles and zeros in the
z-domain, the impulse response \(h[n]\) in the \(n\)-domain,
and the frequency
response \(H(e^{j\hat\omega})\) (the \(\hat\omega\)-domain). A
graphical user interface (GUI) called
PeZ was written in MATLAB
for doing interactive explorations of the three domains.
In this mini-project you will experiment with PeZ to learn the connection
between pole-zero placement and frequency response. Given this information
you will redo the Tone Removal Mini-Project using an IIR.
[Files]
For this mini project you will write a simple function that
listens to a tone and identifies what note it is.
[Files]
For this mini project you will write a simple function that
listens to a wav file of a simple song and identifies
the notes being played.
The wav files have some simple songs on which you can practice.
[Files]
You have gotten to the point in your studies that you can
understand DSP papers that appear in IEEE publications.
The purpose of this project is to read one such paper
and reproduce some of its results.
The goal of this mini-project is to help you understand a simple modem, the FSK modem, referred to by the International Telecommunications Union (ITU) as V.21.
The goal of this mini-project is to build a simple modem receiver. This a follow on for the previous mini-project.
DSP First 2e
McClellan, Schafer, Yoder
ISBN-10: 0136019250 • ISBN-13: 9780136019251
© 2016 Pearson Education, Inc.