Introduction to FIR filtering
FIR filters use a running weighted average to form the output from the
input. In this demo we use a 5-point averager which computes the
output \(y[n] \) from the input \(x[n]\) via the difference
equation:
$$y[n] = \frac{x[n] + x[n-1] + x[n-2] + x[n-3] + x[n-4]}5$$
You can listen to the input signal that
will be passed through the 5-point averager.
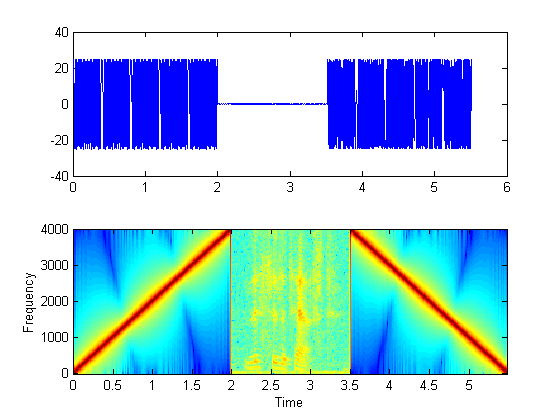
Below is the time-domain plot and the spectrum of the input signal. Do they make sense?
Here is the frequency response of the 5-point averager.
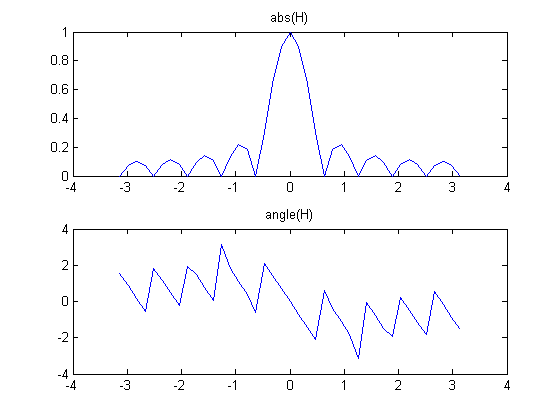
It lets the lower frequencies pass through and attenuates (makes softer) the higher frequencies. Some frequencies are completely removed. Which ones are they? Listen to the signal after filtering.
Compare to the input signal. Why do they differ? Can you hear where the frequencies are missing?
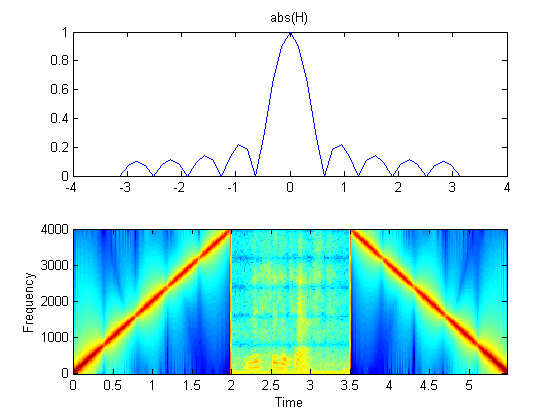
Below is the spectrum of the output signal (red and dark red indicate the largest values, while green and blue are small). Can you see which frequencies have been removed?
Below is the time-domain plot and the spectrum of the input signal. Do they make sense?
Here is the frequency response of the 5-point averager.
It lets the lower frequencies pass through and attenuates (makes softer) the higher frequencies. Some frequencies are completely removed. Which ones are they? Listen to the signal after filtering.
Compare to the input signal. Why do they differ? Can you hear where the frequencies are missing?
Below is the spectrum of the output signal (red and dark red indicate the largest values, while green and blue are small). Can you see which frequencies have been removed?
DSP First 2e
McClellan, Schafer, Yoder
ISBN-10: 0136019250 • ISBN-13: 9780136019251
© 2016 Pearson Education, Inc.