There is a simple graphical relationship between the
z-plane and the frequency response of a filter.
For example, if the transfer function of a system is: $$H(z)=\frac1{1 - 2r \cos(\theta)z^{-1} + r^2 z^{-2}}$$ with \(r=0.97\) and \(\theta=\frac23 \pi\). Multiply top and bottom by \(z^2\) to get: $$H(z)=\frac{z^2}{z^2 - 2r \cos(\theta)z + r^2}$$ What are the poles and zeros of this \(H(z)\)? Will \(r\) and \(\theta\) be the radius and angle of a pole?
Note: the transfer function above can be written with the symbolic toolbox in MATLAB:
Here is how you can get MATLAB to show you the poles and zeros. First, express the numerator as a polynomial, then find its roots to get the zeros:
Now check for the poles by finding the roots of the denominator polynomial:
The two poles have a magnitude of 0.97 and their angles are +120 degrees and -120 degrees. Figure 1 is a plot of the pole locations and zero locations in the complex Z-plane.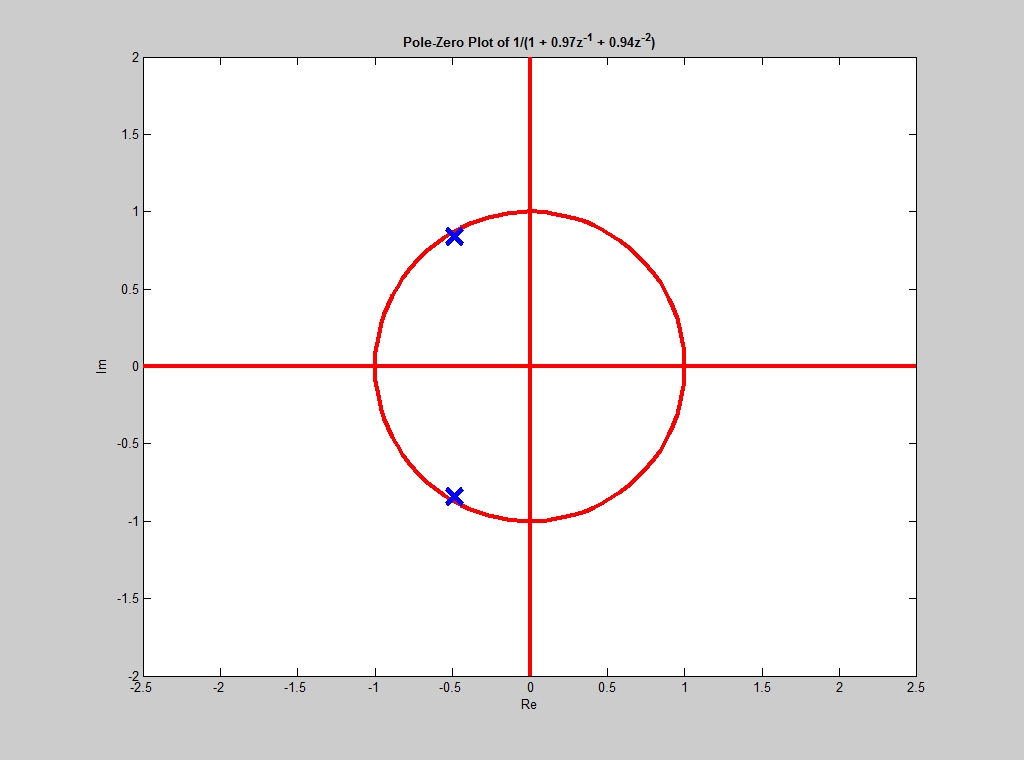
Figure 1. Pole-Zero plot of \(H(z)=\frac1{1+0.97z^{-1}+0.9409z^{-2}}\)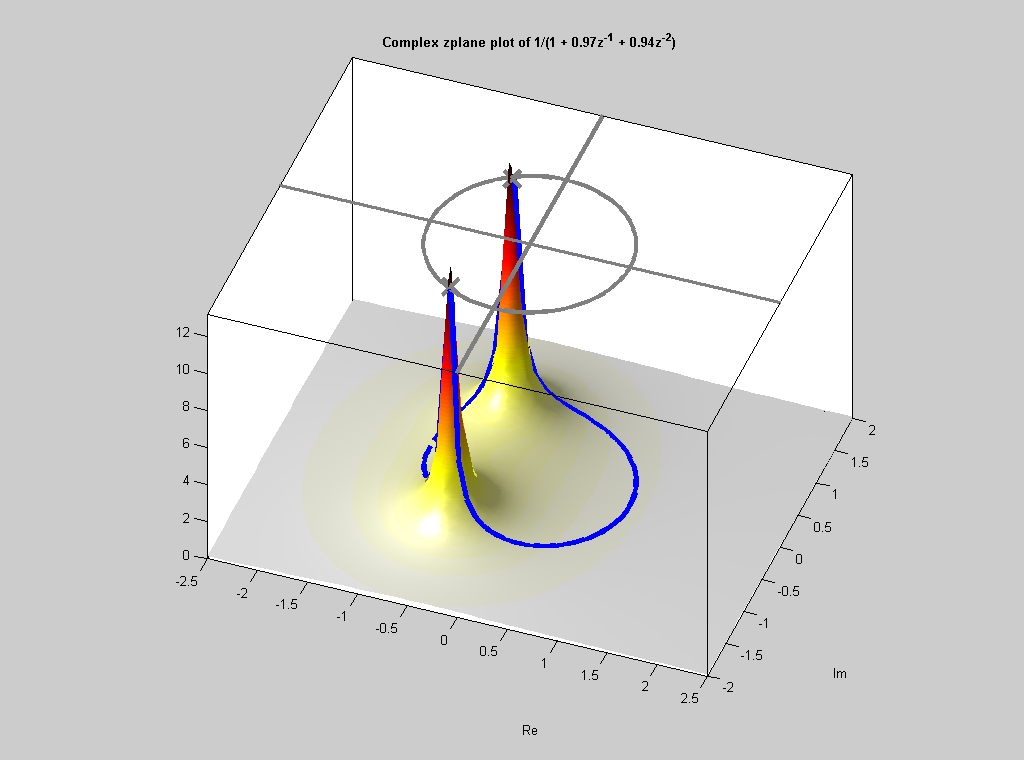
Figure 2. 3D surface plot of \(H(z)=\frac1{1+0.97z^{-1}+0.9409z^{-2}}\) Are the poles and zeros where they should be, based on factoring the polynomials? Figure 2 is a 3D plot of \(H(z)\) over the entire complex Z-plane. You can see the two peaks caused by the poles and the valley in between formed by the zeros at \(z=0\). The frequency response is is found by evaluating \(H(z)\) along the contour defined by \(z\) equal \(e^{j\hat\omega}\). In Figure 1, the unit circle is given for reference; the two poles lie just inside the unit circle. Figure 2 shows a blue line that traces out the unit circle.
The frequency response is the curve you get if you ride a bike along the unit circle and plot your altitute. Figure 3 is the frequency response of \(H(z)\).

Figure 3. Frequency Response plot of \(H(z)=\frac1{1+0.97z^{-1}+0.9409z^{-2}}\)
Figure 4 is a movie showing how the frequency response is found by tracing around the unit circle.
Figure 4. Movie
Here is another movie to help you visualize what is happening
For example, if the transfer function of a system is: $$H(z)=\frac1{1 - 2r \cos(\theta)z^{-1} + r^2 z^{-2}}$$ with \(r=0.97\) and \(\theta=\frac23 \pi\). Multiply top and bottom by \(z^2\) to get: $$H(z)=\frac{z^2}{z^2 - 2r \cos(\theta)z + r^2}$$ What are the poles and zeros of this \(H(z)\)? Will \(r\) and \(\theta\) be the radius and angle of a pole?
Note: the transfer function above can be written with the symbolic toolbox in MATLAB:
EDU>> Hz = sym('1/( 1 - 2*r*cos(ang)*z^(-1) + r^2*z^(-2))')
Hz =
1/( 1 - 2*r*cos(ang)*z^(-1) + r^2*z^(-2) )
EDU>>pretty(Hz)
Here is how you can get MATLAB to show you the poles and zeros. First, express the numerator as a polynomial, then find its roots to get the zeros:
EDU>>numerator = [1 0 0]
numerator =
1 0 0
EDU>>roots(numerator)
ans =
0
0
So the zeros are both at \(z=0\).
Now check for the poles by finding the roots of the denominator polynomial:
EDU>>r = 0.97;
EDU>>ang = 2*pi/3;
EDU>>denominator = [1 -2*r*cos(ang) r^2]
denominator =
1.0000 0.9700 0.9409
EDU>>roots(denominator)
ans =
-0.4850 + 0.8400i
-0.4850 - 0.8400i
EDU>>zprint(ans)
Z = X + jY Magnitude Phase Ph/pi Ph(deg)
-0.485 0.84 0.97 2.094 0.667 120.00
-0.485 -0.84 0.97 -2.094 -0.667 -120.00
EDU>>zplane(numerator, denominator);
EDU>>axis([xmin xmax ymin ymax]);
The two poles have a magnitude of 0.97 and their angles are +120 degrees and -120 degrees. Figure 1 is a plot of the pole locations and zero locations in the complex Z-plane.

Figure 1. Pole-Zero plot of \(H(z)=\frac1{1+0.97z^{-1}+0.9409z^{-2}}\)

Figure 2. 3D surface plot of \(H(z)=\frac1{1+0.97z^{-1}+0.9409z^{-2}}\) Are the poles and zeros where they should be, based on factoring the polynomials? Figure 2 is a 3D plot of \(H(z)\) over the entire complex Z-plane. You can see the two peaks caused by the poles and the valley in between formed by the zeros at \(z=0\). The frequency response is is found by evaluating \(H(z)\) along the contour defined by \(z\) equal \(e^{j\hat\omega}\). In Figure 1, the unit circle is given for reference; the two poles lie just inside the unit circle. Figure 2 shows a blue line that traces out the unit circle.
The frequency response is the curve you get if you ride a bike along the unit circle and plot your altitute. Figure 3 is the frequency response of \(H(z)\).

Figure 3. Frequency Response plot of \(H(z)=\frac1{1+0.97z^{-1}+0.9409z^{-2}}\)
Figure 4 is a movie showing how the frequency response is found by tracing around the unit circle.
Figure 4. Movie
Here is another movie to help you visualize what is happening
