9. <i>z</i>-Transforms

9. z-Transforms

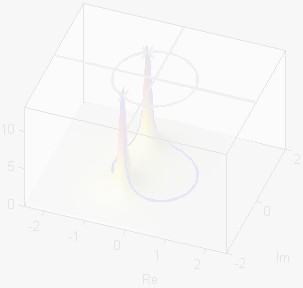
Overview: In this chapter the \(z\)-Transform is introduced for FIR filters. This algebraic method introduces polynomials into the analysis of linear time-invariant (LTI) systems. Thus the well-known operations of factoring of polynomials, multiplying and dividing polynomials have powerful consequences and interpretations for digital filters. In general, the \(z\)-Transform system functions are rational functions-the ratio being a numerator polynomial divided by a denominator polynomial. Of particular interest are the polynomial roots which, in the case of feedback filters, make up the poles and zeros of the filter. In the long run, most properties of digital filters can be restated in terms of the pole and zero locations in the complex \(z\)-plane. For example, stability of a filter requires that the poles lie inside the unit circle.

Databases: Labs Examples Exercises Homework Search

Demos - MATLAB 3

PeZ GUI

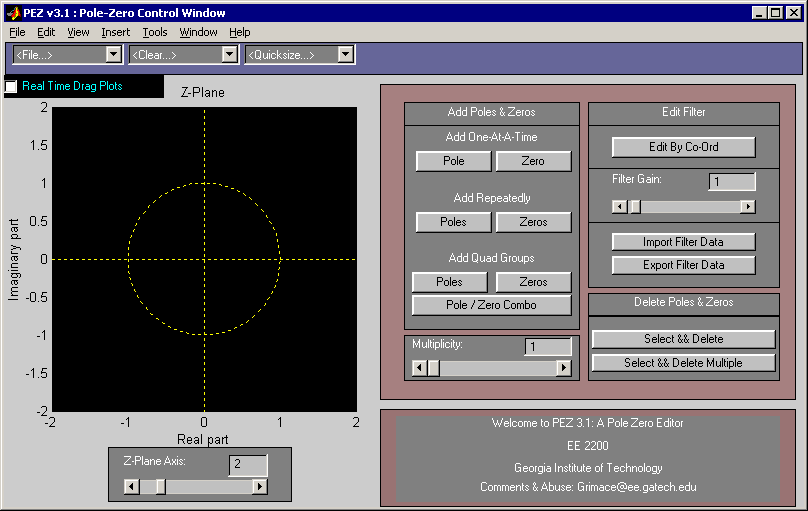
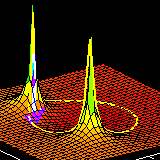
PeZ (pezdemo) is a MATLAB tool for pole/zero manipulation. Poles and zeros can be placed anywhere on a map of the \(z\)-plane. The corresponding time domain (\(n\)) and frequency domain (\(\hat\omega\)) plots will be displayed. When a zero pair (or pole pair) is dragged, the impulse response and frequency response plots will be updated in real time.

Three Domains - FIR

The connection between the Z-transform domain of poles and zeros and the time domain, and also the frequency domain is illustrated with several movies where individual zeros or zero pairs are moved continuously.

Z to Freq

A demo that illustrates the connection between the complex \(z\)-plane and the frequency response of a system. The frequency response is obtained by evaluating \(H(z)\) on the unit circle in the complex \(z\)-plane.

Labs - MATLAB 2

P-13: Encoding and Decoding Touch-Tone (DTMF) Signals

This lab introduces a practical application where sinusoidal signals are used to transmit information: a touch-tone dialer. Bandpass FIR filters can be used to extract the information encoded in the waveforms. The goal of this lab is to design and implement bandpass FIR filters in M ATLAB , and to do the decoding automatically. In the experiments of this lab, you will use firfilt(), or conv(), to implement filters and freqz() to obtain the filter’s frequency response. 1 As a result, you should learn how to characterize a filter by knowing how it reacts to different frequency components in the input. [Files]

P-14: Octave Band Filtering

This lab introduces a practical application where we attempt to extract information from sinusoidal signals - in this case, piano notes. Bandpass FIR filters can be used to extract the information encoded in the waveforms. The goal of this lab is to design and implement several bandpass FIR filters in MATLAB, and use the filtered outputs to determine automatically which note is being played. However, since there are 88 keys on the piano, we will only require the system to figure out which octave the note is in, not the exact note. In the experiments of this lab, you will use firfilt(), or conv(), to implement filters and freqz() to obtain the filter's frequency response. As a result, you should learn how to characterize a filter by knowing how it reacts to different frequency components in the input. [Files]