Overview: In chapter three, the graphical representation of signals
via their frequency content is treated. Previously, we learned
about the properties of sinusoidal waveforms of the form:
$$x(t)=A \cos(2\pi f_0 t + \varphi) = \Re \left\{A e^{j \varphi} e^{j2\pi f_0 t}\right\}$$
In this chapter, we will also show how to synthesize more complicated sinusoidal waveforms
composed of sums of sinusoidal signals, each with a different frequency
(\(f_k\))
$$x(t) = \sum_{k=1}^N A_k \cos(2\pi f_kt + \varphi_k) = \Re \left\{\sum_{k=1}^N Z_k e^{j 2\pi f_k t}\right\}$$
where \(Z_k = A_k e^{j \varphi_k}\) is the complex (phasor) amplitude.
Finally, some signals whose frequency changes with time will be studied, e.g., chirp signals which are based on linear frequency modulation (LFM).
Demos - MATLAB 6
This demo shows the interesting situation that occurs when we have two sinusoidal signals of slightly different frequencies.
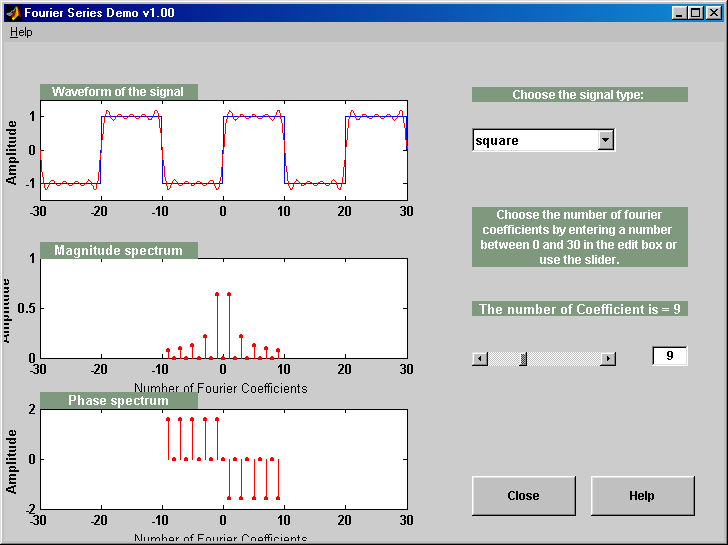
This MATLAB demo reconstructs a square, triangle, or
sawtooth waveform, using a given number of Fourier Series coefficients.
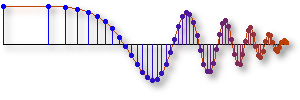
This demonstrates the idea of harmonic sinusoids.
Five sinusoids with a common fundamental frequency are
added together, one at a time.
Demos - LabVIEW 3
Shows the effect of multiplying two sinusoids that are close in frequency.
Shows how any periodic signal can be approximated as a sum of sinusoids.
It allows you to choose from several input signals and creates an approximati on
to the signal you choose.
You can select how mnay cosine terms to use in the approximation.
Labs - MATLAB 7
In this lab, we will synthesize more complicated sinusoidal waveforms
composed of sums of sinusoidal signals, each with a different
frequency. The sounds synthesized will one of several songs.
[Files]
In this lab, we will synthesize more complicated sinusoidal waveforms
composed of sums of sinusoidal signals, each with a different
frequency. The sounds synthesized will sound like a voice.
[Files]
The objective of this lab is to introduce more complicated
signals that are related to the basic sinusoid.
These are signals which implement frequency modulation (FM) and
amplitude modulation (AM) are widely used in communication systems
such as radio and television, but they also can be used to create
interesting sounds that mimic musical instruments.
This lab includes a project on sound synthesis with sinusoids. The sound synthesis will be done with
sinusoidal waveforms of the form
$$ x(t) = \sum_k A_k \cos(\omega_k t + \phi_k)
$$
where the amplitudes can be manipulated to produce a musical illusion. The challenge of the lab is to adjust
the amplitudes to improve the subjective quality for listening.
The objective of this lab is to introduce more complicated signals that
are related to the basic sinusoid.
These are signals which implement frequency modulation (FM) and
amplitude modulation (AM) are widely used in communication systems
such as radio and television, but they also can be used to create
interesting sounds that mimic musical instruments.
[Files]
The objective of this lab is to introduce more complicated signals that are related to the basic sinusoid.
These signals which implement frequency modulation (FM) and amplitude modulation (AM) are widely used in
communication systems such as radio and television. In addition, they can be used to create interesting
sounds that mimic musical instruments. The resulting signal
can be analyzed to show its time-frequency behavior by using the spectrogram.
This lab studies signal synthesis for AM and FM signals, and their time-frequency content as shown in
a spectrogram. An underlying objective of the lab is to learn more about the spectrogram.
In this lab, we will synthesize more complicated sinusoidal waveforms
composed of sums of sinusoidal signals, each with a different
frequency. The sounds synthesized will one of several songs.
Labs - LabVIEW 5
The objective of this lab is to introduce more complicated
signals that are related to the basic sinusoid.
These are signals which implement frequency modulation (FM) and
amplitude modulation (AM) are widely used in communication systems
such as radio and television, but they also can be used to create
interesting sounds that mimic musical instruments.
In this lab, we will synthesize more complicated sinusoidal waveforms
composed of sums of sinusoidal signals, each with a different
frequency. The sounds synthesized will one of several songs.
[Files]
This lab includes a project on speech synthesis with sinusoids. The speech synthesis will be done with sinusoidal waveforms where each sinusoid will have short duration on the order of the pitch period of the speaker. One objective of this lab is to study how many sinusoids are needed to create a sentence that sounds good. A secondary objective of the lab is the challenge of putting together the short duration sinusoids without introducing artifacts at the transition times. Finally, much of the understanding needed for this lab involves the spectral representation of signals - a topic that underlies this entire course.
[Files]
The objective of this lab is to introduce more complicated signals that
are related to the basic sinusoid.
These are signals which implement frequency modulation (FM) and
amplitude modulation (AM) are widely used in communication systems
such as radio and television), but they also can be used to create
interesting sounds that mimic musical instruments.
[Files]
In this lab, we will synthesize more complicated sinusoidal waveforms
composed of sums of sinusoidal signals, each with a different
frequency. The sounds synthesized will one of several songs.