In this lab we introduce the fundamentals of Matlab. Matlab is
a programming environment that you will find helpful for many of
the exercises in this text.
Manipulating sinusoid functions using complex exponentials turns
trigonometric problems into simple arithmetic and algebra.
In this lab, we first review the complex exponential signal and the
phasor addition property needed for adding cosine waves.
Then we will use Matlab to make plots of phasor diagrams that show
the vector addition needed when combining sinusoids.
Manipulating sinusoid functions using complex exponentials turns
trigonometric problems into simple arithmetic and algebra.
In this lab, we first review the complex exponential signal and the
phasor addition property needed for adding cosine waves.
Then we will use Matlab to make plots of phasor diagrams that show
the vector addition needed when combining sinusoids.
[Files]
The objective of this lab is to learn how the outputs from two spatially separated sensors that
receive signals from the same source can be used to estimate the direction to the source of the signal. The
key to this processing is phase difference or time difference of arrival (TDOA) at the two receivers.
[Files]
In this lab, we will synthesize more complicated sinusoidal waveforms
composed of sums of sinusoidal signals, each with a different
frequency. The sounds synthesized will one of several songs.
[Files]
In this lab, we will synthesize more complicated sinusoidal waveforms
composed of sums of sinusoidal signals, each with a different
frequency. The sounds synthesized will sound like a voice.
[Files]
The objective of this lab is to introduce more complicated
signals that are related to the basic sinusoid.
These are signals which implement frequency modulation (FM) and
amplitude modulation (AM) are widely used in communication systems
such as radio and television, but they also can be used to create
interesting sounds that mimic musical instruments.
This lab includes a project on sound synthesis with sinusoids. The sound synthesis will be done with
sinusoidal waveforms of the form
$$ x(t) = \sum_k A_k \cos(\omega_k t + \phi_k)
$$
where the amplitudes can be manipulated to produce a musical illusion. The challenge of the lab is to adjust
the amplitudes to improve the subjective quality for listening.
The objective of this lab is to introduce more complicated signals that
are related to the basic sinusoid.
These are signals which implement frequency modulation (FM) and
amplitude modulation (AM) are widely used in communication systems
such as radio and television, but they also can be used to create
interesting sounds that mimic musical instruments.
[Files]
The objective of this lab is to introduce more complicated signals that are related to the basic sinusoid.
These signals which implement frequency modulation (FM) and amplitude modulation (AM) are widely used in
communication systems such as radio and television. In addition, they can be used to create interesting
sounds that mimic musical instruments. The resulting signal
can be analyzed to show its time-frequency behavior by using the spectrogram.
This lab studies signal synthesis for AM and FM signals, and their time-frequency content as shown in
a spectrogram. An underlying objective of the lab is to learn more about the spectrogram.
In this lab, we will synthesize more complicated sinusoidal waveforms
composed of sums of sinusoidal signals, each with a different
frequency. The sounds synthesized will one of several songs.
The objective in this lab is to introduce digital images as a
second useful signal type. We will show how the
A-to-D sampling and the D-to-A reconstruction processes are
carried out for digital images. In particular,
we will show a commonly used method of image zooming
(reconstruction) that gives poor results a later
lab will revisit this issue and do a better job.
[Files]
The objective of this lab is to study further the spectral content of signals analyzed via the spectrogram.
There are several specific steps that will be considered in this lab:
- Synthesize a linear-FM chirp with a Matlab M-file, and display its spectrogram. Choose the chirp parameters so that aliasing will happen.
- Synthesize a periodic triangle wave with a Matlab M-file, and display its spectrogram. Relate the harmonic line spectrum to the fundamental period of the triangle wave.
- Compare spectrograms using different scales for amplitude: decibels (dB) for amplitude versus linear amplitude.
- Examine details of the harmonic lines in the dB spectrogram of the triangle wave.
- Spectrogram: make a spectrogram of your voice signal, and relate the harmonic line spectrum to your previous measurement of pitch period.
The goal of this lab is to learn how to implement FIR filters
in Matlab, and then study the response of FIR
filters to various signals, including images and speech.
As a result, you should learn how filters can create
interesting effects such as blurring and echoes. In addition,
we will use FIR filters to study the convolution
operation and properties such as linearity and time-invariance.
[Files]
The goal of this lab is to learn how to implement FIR filters in Matlab, and then study the response of FIR
filters to various signals, including images or speech.
[Files]
The goal of this lab is to learn how to implement FIR filters in Matlab, and then study the response of FIR
filters to various signals, including images or speech.
This mini project concentrates on the use of
dconvdemo a GUI for discrete-time convolution.
This demo is exactly the same as the Matlab functions conv()
and firfilt() used to implement FIR filters.
This demo illustrates an important point about the behavior of a linear, time-invariant (LTI) system. It also
provide a convenient way to visualize the output of a LTI system.
The goal of this lab is to study the frequency response. For FIR filters this is the response to inputs such as
complex exponentials and sinusoids. You can use
firfilt(), or conv(), to implement filters and freqz()
to obtain the filter’s frequency response. As a result, you should learn how to characterize a filter by
knowing how it reacts to different frequency components in the input.
The goal of this lab is to study the response of FIR filters to
inputs such as complex exponentials and
sinusoids. In the experiments of this lab, you will use
firfilt(),
or conv(), to implement filters and
freqz() to obtain the filter's frequency response.
As a result, you should learn how to characterize a
filter by knowing how it reacts to different frequency components
in the input.
This lab also introduces two practical filters: bandpass filters
and nulling filters. Bandpass filters can be
used to detect and extract information from sinusoidal signals, e.g.,
tones in a touch-tone telephone dialer.
Nulling filters can be used to remove sinusoidal interference, e.g.,
jamming signals in a radar.
The goal of this lab is to study the sinusoidal response of some simple FIR filters in Matlab.
This leads to a study of the frequency response function.
In the experiments of this lab, you will use the Matlab GUI called
dltidemo to find the frequency
response function for FIR filters.
[Files]
In this mini-project you will write a simple Matlab
program that removes unwanted tones from a wav file.
The file
SunshineSquare.wav has had some unwanted tones added to it.
Your job is to remove the tones so you can hear the message better.
[Files]
This lab introduces a practical application where sinusoidal signals are used to transmit information: a
touch-tone dialer. Bandpass FIR filters can be used to extract the information encoded in the waveforms.
The goal of this lab is to design and implement bandpass FIR filters in M ATLAB , and to do the decoding
automatically. In the experiments of this lab, you will use
firfilt(), or conv(), to implement filters and
freqz() to obtain the filter’s frequency response. 1 As a result, you should learn how to characterize a filter
by knowing how it reacts to different frequency components in the input.
[Files]
The goal of this lab is to learn some methods for designing practical FIR filters in Matlab. These filters
will have a finite number of coefficients, and a frequency response that approximates an ideal frequency
response shape.
The objective of this lab is to introduce more complicated signals that are related to the basic sinusoid.
These signals which implement frequency modulation (FM) and amplitude modulation (AM) are widely used in
communication systems such as radio and television. In addition, they can be used to create interesting
sounds that mimic musical instruments. The resulting signal
can be analyzed to show its time-frequency behavior by using the spectrogram.
This lab studies signal synthesis for AM and FM signals, and their time-frequency content as shown in
a spectrogram. An underlying objective of the lab is to learn more about the spectrogram.
The objective of this lab is to study further the spectral content of signals analyzed via the spectrogram.
There are several specific steps that will be considered in this lab:
- Synthesize a linear-FM chirp with a Matlab M-file, and display its spectrogram. Choose the chirp parameters so that aliasing will happen.
- Synthesize a periodic triangle wave with a Matlab M-file, and display its spectrogram. Relate the harmonic line spectrum to the fundamental period of the triangle wave.
- Compare spectrograms using different scales for amplitude: decibels (dB) for amplitude versus linear amplitude.
- Examine details of the harmonic lines in the dB spectrogram of the triangle wave.
- Spectrogram: make a spectrogram of your voice signal, and relate the harmonic line spectrum to your previous measurement of pitch period.
This lab introduces a practical application where sinusoidal signals are used to transmit information: a
touch-tone dialer. Bandpass FIR filters can be used to extract the information encoded in the waveforms.
The goal of this lab is to design and implement bandpass FIR filters in Matlab, and to do the decoding
automatically. In the experiments of this lab, you will use
firfilt(), or conv(), to implement filters and
freqz() to obtain the filter’s frequency response. As a result, you should learn how to characterize a filter
by knowing how it reacts to different frequency components in the input.
[Files]
This lab introduces a practical application where we attempt
to extract information from sinusoidal signals -
in this case, piano notes. Bandpass FIR filters can be
used to extract the information encoded in the waveforms.
The goal of this lab is to design and implement several
bandpass FIR filters in Matlab, and use the
filtered outputs to determine automatically which note is being played.
However, since there are 88 keys on
the piano, we will only require the system to figure
out which octave the note is in, not the exact note. In
the experiments of this lab, you will use
firfilt(), or conv(),
to implement filters and freqz() to
obtain the filter's frequency response. As a result,
you should learn how to characterize a filter by knowing
how it reacts to different frequency components in the input.
[Files]
The objective for this lab is to build an intuitive understanding of
the relationship between the location of poles and zeros in the
z-domain, the impulse response \(h[n]\) in the \(n\)-domain,
and the frequency
response \(H(e^{j\hat\omega})\) (the \(\hat\omega\)-domain). A
graphical user interface (GUI) called
PeZ was written in MATLAB
for doing interactive explorations of the three domains.
The goal of this lab is to explore the connection between the time domain \((n)\), the frequency domain (\(\hat\omega\)),
and the \(z\)-transform domain, using the GUI PeZ in Matlab.
- Placing Zeros: When placed on the unit circle, zeros of the numerator \(B(z)\) will force the frequency response to be zero which can then be used to null out sinusoids at one frequency.
- Placing Poles: When placed near the unit circle (but inside), roots of denominator \(A(z)\) will create peaks in the frequency response which can be used to form BPFs.
- Designing IIR Notch Filters: requires conjugate zeros on the unit circle (UC) with a poles at the same angle, just inside the UC. The frequency response of the notch is much sharper than a nulling filter which is an FIR filter formed only from the conjugate zeros on the UC.
In this mini-project you will experiment with PeZ to learn the connection
between pole-zero placement and frequency response. Given this information
you will redo the Tone Removal Mini-Project using an IIR.
For this mini project you will write a simple function that
listens to a tone and identifies what note it is.
[Files]
For this mini project you will write a simple function that
listens to a wav file of a simple song and identifies
the notes being played.
The wav files have some simple songs on which you can practice.
[Files]
You have gotten to the point in your studies that you can
understand DSP papers that appear in IEEE publications.
The purpose of this project is to read one such paper
and reproduce some of its results.

 1. Introduction
1. Introduction 2. Sinusoids
2. Sinusoids 3. Spectrum Representation
3. Spectrum Representation 4. Sampling and Aliasing
4. Sampling and Aliasing 5. FIR Filters
5. FIR Filters 6. Frequency Response of FIR Filters
6. Frequency Response of FIR Filters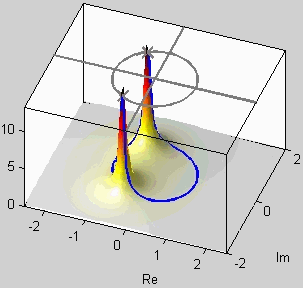 9. z-Transforms
9. z-Transforms 10. IIR Filters
10. IIR Filters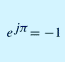 A. Complex Numbers
A. Complex Numbers